My statistical research is in the areas of computer experiments, computer model calibration, uncertainty quantification and statistical methods for large datastructures aka “big data”. Most of the applied problems that have motivated my statistical research have originated from climate/environmental science and physics. I am also interested in leveraging mathematical models and observational data to understand environmental impacts on health. More recently, I have become obsessively interested in blockchain technology and decentralization. This was the result of finally having some time to learn new things during the pandemic (silver lining!), and I went down the proverbial rabbit hole.
You can view my CV here.
Current Research
My current research is continuing in the directions I have embarked on over the past few years: we are investigating further improvements to MCMC sampling for Bayesian regression trees, new ideas in discrepancy for computer model calibration motivated by applications in nuclear physics and biochemical reaction networks, and investigating the importance of measuring influence in BART.
My current research is supported by a generous KAUST CRG grant with Dr. Ying Sun and Dr. Brian Reich, a generous NSF grant with Dr. Rob McCulloch and Dr. Ed George, and a generous NSF grant as part of the BAND project. Thank you for your support!
Ongoing Projects
John Yannotty: Bayesian Treed Model Mixing, joint work with Dr. Tom Santner
Vincent Geels: Tree-based count data models, joint work with Dr. Radu Herbei
Influence and outliers in BART – joint work with Dr. Rob McCulloch and Dr. Ed George
Vincent Geels: The Taxicab Sampler, joint work with Dr. Radu Herbei
A Bayesian Framework for Quantifying Model Uncertainties in Nuclear Dynamics – joint work with D.R. Phillips and the BAND project team.
Designing Optimal Experiments in Proton Compton Scattering – J.A. Melendez’s thesis work in Physics, supervisor: R.A. Furnstahl
Akira Horiguchi: Pareto Front Optimization with BART, joint work with Dr. Tom Santner and Dr. Ying Sun
Quantifying Correlated Truncation Errors in EFT models – J.A. Melendez’s thesis work in Physics, supervisor: R.A. Furnstahl
Akira Horiguchi: Variable Importance for BART with Dr. Tom Santner
Gavin Collins: Somewhat Smarter Learners for BART with Dr. Rob McCulloch and Dr. Ed George
Adaptive Resolution BART for Image Data aka “the beach project” with Dr. Dave Higdon
Multivariate BART with Dr. Ying Sun and Dr. Wu Wang
The infamous Dream Project
2022
Influence in BART: Typically in modern statistical and machine learning models one does not consider the effect of influential or outlier observations on the fitted model. Does it matter? Our work shows that it indeed does, and we explore some diagnostics to screen for such problematic observations, and then propose an importance sampling algorithm to re-weight the posterior draws given the identified observations.
Multi-tree models for count data: The second project from Vincent’s thesis, and really cool creative work. Instead of introducing n latent continuous variable to facilitate modeling non-Gaussian data in the Bayesian tree setting, Vincent introduces a one-to-many transformation to facilitate the modeling of count data, which only introduces q<<n latents.
Bayesian Treed Model Mixing: The first project from John’s thesis work, we use Bayesian trees to facilitate the construction of a model to perform model-mixing of multiple Physics simulators where the simulators have varying utility depending on the region of input space.
Optimally Batched Bayesian Trees: Another joint project with Luo, this idea is incredibly cool. More soon…
2021
The Taxicab Sampler: In this work, Vincent considers modeling count data directly rather than by the standard transformation/link function approach. This motivates the need for an efficient MCMC sampler for a discrete, countable random variable. The solution – the Taxicab sampler – is motivated by the so-called Hamming Ball sampler which also considers sampling a discrete data object, but in that case only targets 0/1 type random variables.
Pareto Front Optimization with BART: We explore a BART-based model for performing Pareto Front optimization. Our approach models multiple response functions as independent BART ensembles, then constructs an estimator for the Pareto Front and Pareto Set, and includes uncertainty information for both. The code for this has been implemented in the OpenBT source.
2020
A Bayesian Framework for Quantifying Model Uncertainties in Nuclear Dynamics: The so-called “manifesto” paper, outlining the broad vision/goals of the BAND project. The particular contribution of my group is considering so-called Bayesian Model Mixing as a generalization of model averaging, and drawing connections from this idea to the popular Kennedy-O’Hagan framework of Model Calibration.
Variable Importance for BART: In the first part of Akira’s Ph.D. thesis we arrive at a closed-form construction for calculating Sobol’ sensitivity indices in tree (e.g. BART) models. The code for this has been implemented in the OpenBT source.
Designing Optimal Experiments in Proton Compton Scattering: More work with Melendez and Furnstahl, essentially now adding an optimal experimental design construction to the EFT expansion emulator explored in the first paper.
2019
Near-Optimal Design: In this joint work with Dr. Craigmile, we explore new ideas in near-optimal design with our awesome Ph.D. student Sophie Nguyen (now at JP Morgan Chase). In challenging optimization problems, how good is our numerical approximation of the true underlying optimum?
Sparse Additive Gaussian Process Regression: A super fun “side-project” with Hengrui Luo and Giovanni Nattino that grew out of their project during my special topics course. We borrow ideas of sparsity and localization to propose a new Gaussian Process regression model for big data in the Bayesian setting. A key component is a novel recursive partitioning scheme that only depends on the predictors. An arXiv preprint has been posted!
Quantifying Correlated Truncation Errors in EFT models: This very cool work done by Jordan Melendez, a Ph.D. student of Richard Furnstahl, looks at GP-based emulation of a nuclear model that explicitly builds on a theoretically derived multi-scale approximation, allowing appropriate uncertainty quantification when emulating such models. Joint with Daniel Phillips and Sarah Wesolowski, to appear in Physical Review C.
BDMCMC for BART: Joint work with Dr. Reza Mohammadi and Dr. Maurits Kaptein on a birth-death sampler for BART. This is a fancy technique that Reza had applied previously in graphical models. Mostly performed during summer 2018 while I visited the JADS institute, many thanks to Maurits!
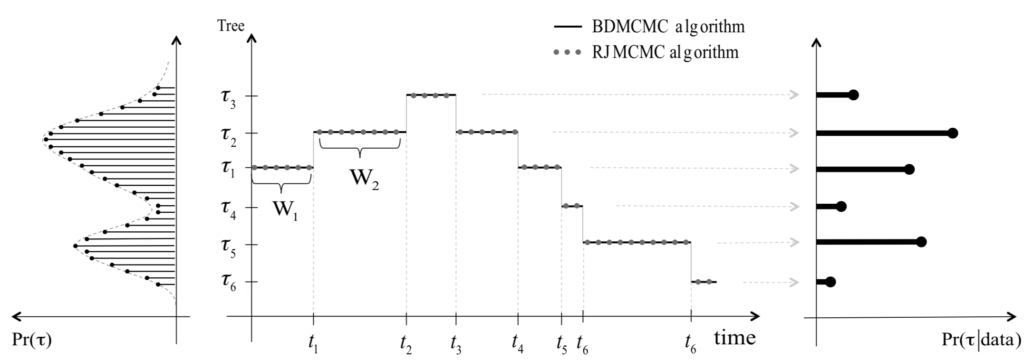
2018
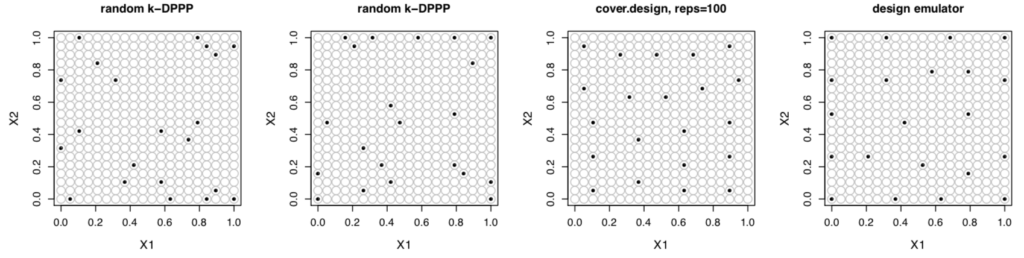
Optimal Design Emulators: a Point Process Approach: Constructing optimal experimental designs is a challenging optimization problem. In this work, instead of viewing the problem from the perspective of optimization, we construct a stochastic process whose mode corresponds to the entropy-optimal design of a Gaussian process model and then arrive at a computationally cheap sampling algorithm to draw optimal design realizations via a point-process design emulator. We demonstrate the method on the popular Stochastic Gradient Descent (SGD) algorithm and optimal designs for Gaussian process regression. (submitted; preprint here).
Bayesian Calibration of Multistate Stochastic Simulators: We consider extending computer model calibration of deterministic simulators to the case of stochastic simulators when multiple realizations of a stochastic simulator are available at a small collection of well designed calibration parameter settings. Applying the method to the calibration of an expensive intra-cellular signaling model and a stochastic model of river water temperature. (Appears in Statistica Sinica’s special issue on computer experiments; available here).
2017
Heteroscedastic BART Via Multiplicative Regression Trees: We use tree ensembles to simultaneously learn the mean function and variance function of data under the Gaussian likelihood assumption. Leveraging conjugacy and an sensible calibration of the prior, the model is as simple to setup as the homoscedastic BART model but will allow the data to drive the posterior towards a heteroscedastic solution while quantifying uncertainties. (submitted; preprint here).
Design and Analysis of Experiments on Nonconvex Regions: Motivated by the optimal design of glacial stake networks important in glaciology and climate research, we consider prediction optimal designs for Gaussian process regression when the design region is non-convex. Our approach is based on a transformation idea motivated by manifold learning techniques to embed the non-convex region into a Euclidean space to perform the design, which can then be projected back into the original non-convex space. (Appears in Technometrics).
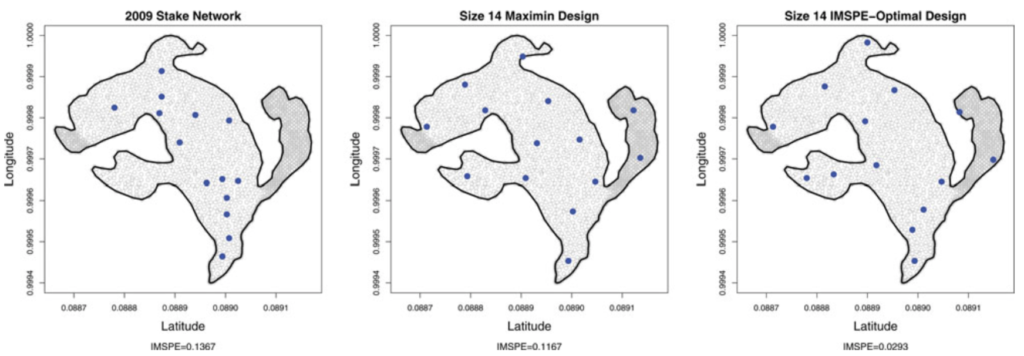
2016
Efficient Proposal Mechanisms for Bayesian Regression Tree Models: in this project we look at some new ways of proposing changes to tree structures in Bayesian regression trees. In applying regression tree approaches to computer experiment problems, the typically small error variance term can lead to poor mixing, resulting in less than nominal coverage of credible intervals for posterior predictions. Our new proposal mechanisms seem to alleviate this problem (Appears in Bayesian Analysis).
BART-based Computer Model Calibration: In another project, we have developed a BART-based Bayesian calibration model that scales to challenging calibration problems. The idea is to learn locally-adaptive bases while retaining efficient MCMC sampling of the posterior distribution. We demonstrate our method by calibrating a radionuclide dispersion model. (Appears in Technometrics).
Utilization of a nonlinear inverse procedure to infer CO2 emissions using limited downwind observations: this is an applied paper where we combine a simulator of the time-evolution of a CO2 plume with a column-integrated observation produced by a Fourier Transform Spectrometer (FTS) sensor.
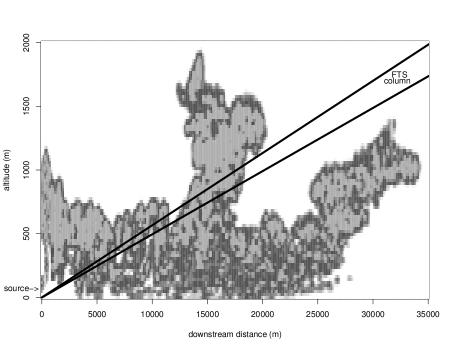
2014
Parallel MCMC sampler for Bayesian Additive Regression Trees: here’s a very interesting and fun project we’ve been working on – a scalable statistical model for big data that doesn’t make any inferential sacrifices. Leverages the very basic statistical ideas of sufficiency and data reduction in a creative way. We also make some technical developments to prove the algorithm’s scalability. (Appears in JCGS).
Dream Project: A side-project started sometime ago looks at quantifying the contribution of outdoor-sourced environmental tobacco smoke on residential indoor air quality and its health impacts in modern cities. Progress is slow, but so important it gets is own page.
2013
Fast Calibration: The main work from my Ph.D. thesis looked at calibrating large and non-stationary computer model output, which was a common feature of the space weather dataset and simulator that motivated our work. (Appears in Technometrics).
Calibration and EKF: We also have done some comparative work involving the usual GP approach to calibration versus ensemble Kalman filter approach which is popular in the data assimilation world. Motivated by applied collaborations involving ice-sheet models, atmospheric models and cosmology models. (Appears in Technometrics).
Applied Motivations: I have been lucky enough to be involved with some great collaborative research that motivates much of my own statistical developments. Two recent collaborations involved investigating the calibration of the CISM ice sheet model and performing statistical inversion of a complex CO2 emission rate problem for international treaty verification.

Ph.D. work
During my Ph.D. I developed new methods for model calibration experiments. Model calibration is an interesting statistical approach that enables scientists or practitioners to investigate a real-world phenomena by combining a simulator of the phenomena with observational data that has been collected. The idea, broadly speaking, is to leverage the simulator to understand the phenomena without requiring extensive observations (they may be expensive, difficult or even dangerous or impossible to collect). And, just to make things a little more challenging, such simulators can usually only be sparsely sampled themselves due to, for example, their computational cost. If that wasn’t enough, it is usually unrealistic to expect the simulator to be a perfect representation of reality, so there is the notion of model bias or discrepancy. The statistical approach of model calibration attempts to account for these various sources of uncertainties while estimating model parameters, constructing predictions and uncertainty bounds, etc.
The first development in my thesis was a practical approach for calibrating large and non-stationary computer model output, which was a common feature of the datasets that were motivating our work. The second development deals with incorporating derivative information from the computer model into a calibration experiment. Many computer models are governed by differential equations, and including this derivative information can be helpful, particularly in small n situations. The final development deals with extending the methodology incorporating derivatives to allow for the inclusion of possible bias in the computer model. The main concern here is whether this bias is identifiable. Our results indicated some modest improvements over the previous approach in some experimental conditions. Well, it is a challenging problem – one that I hope to return to in the next year or so. If some of this sounds interesting, you can see my thesis here.
M.Sc. work
It was during my masters that I was introduced to the very modern area of statistics known as computer experiments or uncertainty quantification. In my project, I worked on constructing optimal designs for a typical statistical model in a non-typical setting – the case where the design space is non-convex. This problem arises in many environmental problems where geography places constraints on the variable of interest, such as contaminants in waterways and streams. The method we came up with was interesting but also computationally expensive, anyhow if you like you can read about it here.
Previously…
In a previous life I was a CS undergrad. In those days, I worked under the supervision of Dr. Thomas Wolf on various problems related to GoTools, a program specializing in solving life & death problems in the game of Go, which resulted in two publications (here and here). I also represented the university twice at the ACM Programming Contest and also won the Brock programming contest once. I also organized an HPC meeting with representatives of Brock University, SHARCNET and AMD. In my upper years, I became very interested in Statistics, and as they say, the rest is history.